백준 1389 : 케빈 베이컨의 6단계 법칙

1. 문제 : https://www.acmicpc.net/problem/1389

1389번: 케빈 베이컨의 6단계 법칙

 

2. 문제 접근

• 노드의 갯수와 간선의 정보가 주어짐. -> 그래프 탐색
• 한 노드에서 다른 모든 노드에 대하여 가장 짧은 경로를 원함. -> Transitive Closure
• 모든 노드에 대해 구해야 함. -> All-Pairs Shortest Paths -> Floyd-Warshall Transitive Closure

 

3. 문제 해결

1. 임의의 한 노드 $K$를 선택. $(K = 1 ... N)$
2. $K$ 노드를 제외한 나머지 두 노드 $I, J$ 선택. $(I = 1 ... N, I != K / J = 1 ... N, J != I, K)$
3. $I$에서 $K$, $K$에서 $J$로 가는 경로가 존재한다면, $I$에서 $J$로 갈 수 있음. (Transitive Closure)
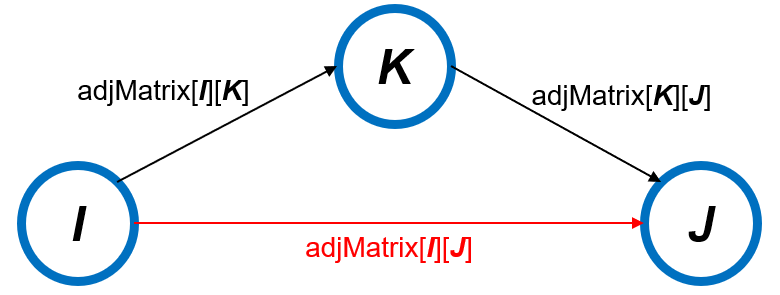
4. $I$에서 $J$로 가는 경로가 없을 경우, 경로 추가.
5. $I$에서 $J$로 가는 경로가 있을 경우, $K$를 거쳐서 가는 경로와 비교하여 더 작은 값으로 수정.

 

4. 코드

#include <iostream>
#include <vector>
using namespace std;

int solution(int N, vector<vector<int>>& relation)
{
	vector<vector<int>> adjMatrix;

	// Initialize the adjacency matrix
	for (int i = 0; i <= N; i++)
	{
		vector<int> temp;

		for (int j = 0; j <= N; j++)
		{
			temp.push_back(0);
		}

		adjMatrix.push_back(temp);
	}

	// Add the edges
	for (int i = 0; i < relation.size(); i++)
	{
		int first = relation[i][0];
		int second = relation[i][1];

		adjMatrix[first][second] = adjMatrix[second][first] = 1;
	}

	// Calculate the number of Kevin Bacon 
	for (int k = 1; k <= N; k++)
	{
		for (int i = 1; i <= N; i++)
		{
			if (i == k) continue;

			for (int j = 1; j <= N; j++)
			{
				if (j == k || j == i) continue;

				if (adjMatrix[i][k] > 0 && adjMatrix[k][j] > 0)
				{
					if (adjMatrix[i][j] == 0) adjMatrix[i][j] = adjMatrix[j][i] = adjMatrix[i][k] + adjMatrix[k][j];
					else adjMatrix[i][j] = adjMatrix[j][i] = min(adjMatrix[i][k] + adjMatrix[k][j], adjMatrix[i][j]);
				}
			}
		}
	}

	// Find the min number 
	int minBacon = 100 * 100;
	int minNumber = 0;
	for (int i = 1; i <= N; i++)
	{
		int bacon = 0;

		for (int j = 1; j <= N; j++)
		{
			if (i == j) continue;

			bacon += adjMatrix[i][j];
		}

		if (minBacon > bacon)
		{
			minBacon = bacon;
			minNumber = i;
		}
	}

	return minNumber;
}

int main()
{
	int N, M;
	vector<vector<int>> relation;
	
	cin >> N >> M;
	
	for (int i = 0; i < M; i++)
	{
		int a, b;
		cin >> a >> b;
		relation.push_back({ a, b });
	}

	cout << solution(N, relation);

	return 0;
}