-
누적합(Prefix Sum)과 차이 배열(Difference Array)문제 해결 기법 2025. 5. 13. 02:30
구간을 빠르게 읽고, 빠르게 업데이트하는 두 가지 핵심 기법
#️⃣ 들어가며
코딩 테스트를 풀다 보면 다음과 같은 요구를 자주 만난다.
- 배열에서 특정 구간의 합을 빠르게 구하라
- 배열의 특정 구간에 여러 번 더해라
해당 문제를 브루트 포스 방식으로 풀 경우 시간 초과가 발생하는 경우가 대다수이다. 전체 배열의 크기를 $N$, 주어진 쿼리의 수가 $M$이라고 할 경우, $O(N \times M)$의 시간이 걸리고, $N$과 $M$은 당연히 매우 큰 숫자가 주어지기 때문이다. 이럴 때 필요한 게 누적합(Prefix Sum)과 차이 배열(Difference Array)다.
1️⃣ 누적합 (Prefix Sum)
📌 정의
누적합(Prefix Sum)은 배열이나 행렬과 같은 자료구조에서, 특정 범위의 합을 빠르게 계산하기 위해 사용하는 전처리 기법이다.
$$prefix[i] \ = \ arr[0] \ + \ arr[1] \ + \cdots \ + \ arr[i]$$
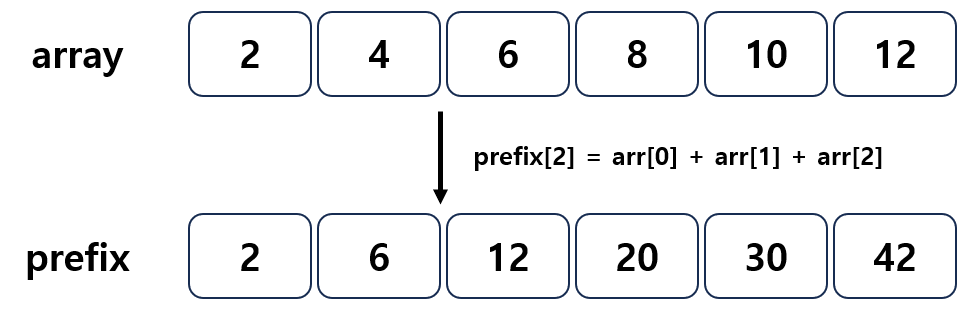
1차원 배열에서 누적합을 계산한 결과 또한 매번 구간의 합을 새로 더하지 않고, 미리 계산한 누적값을 재활용하여 구간 합을 $O(1)$ 시간에 구할 수 있다.
$$sum(i, \ j) \ = \ prefix[j] \ - \ prefix[i \ - \ 1]$$
계산한 누적합을 활용하여 구간합을 계산한 결과 🔨 구현 예제
vector<int> arr = { 2, 4, 6, 8, 10, 12 }; int size = arr.size(); vector<int> prefix(size, 0); // 누적합 초기 세팅 prefix[0] = arr[0]; for (int i = 1; i < size; i++) { prefix[i] = prefix[i - 1] + arr[i]; } // 구간 [2, 4]의 합 : 6 + 8 + 10 = 24 int result = prefix[4] - prefix[2];📊 시간 복잡도
연산 복잡도 누적합 생성 O(N) 구간 합 조회 O(1) 📚 주요 활용처
- 구간 합을 빠르게 구해야 하는 경우
- 배열 값은 바뀌지 않고, 여러 번의 구간 질의(Query)가 있을 때
2️⃣ 차이 배열 (Difference Array)
📌 정의
차이 배열(Difference Array)는 배열이나 행렬과 같은 자료구조에서, 특정 구간에 수를 더하거나 뺄 때 직접 갱신하지 않고 변화량만 기록해두는 방식이다.
$$diff[i] \ = \ arr[i] \ - \ arr[i \ - \ 1]$$
이는 시작 지점과 끝 지점의 다음 칸에 변화량을 기록하는 것으로 구현할 수 있다.
$$diff[x1] \ = \ diff[x1] \ + \ k, \ diff[x2] \ = \ diff[x2] \ - \ k$$
1차원 배열에서 주어진 쿼리에 따라 변화량을 기록한 결과 마지막에 변화량의 누적합을 통해 원래 배열을 복원한다.
$$arr[i] \ = \ diff[0] \ + \ diff[1] \ + \ \cdots \ + \ diff[i]$$
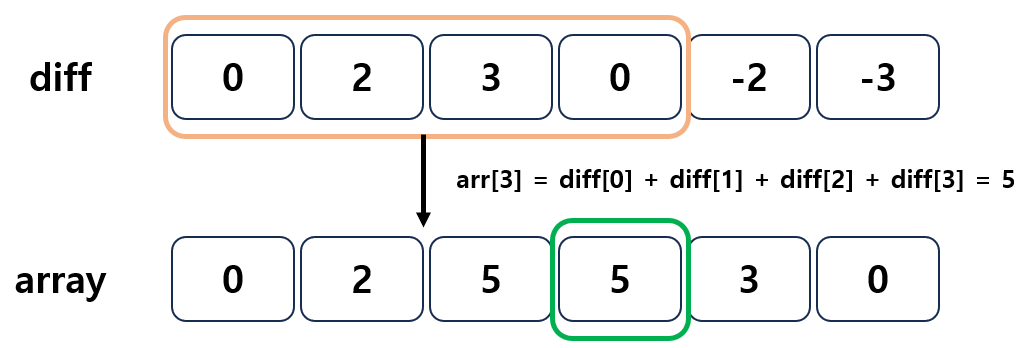
기록한 변화량을 통해 최종 변화량을 계산한 결과 🔨 구현 예제
vector<int> arr = { 0, 0, 0, 0, 0, 0 }; int size = arr.size(); vector<int> diff(size, 0); // 구간 [2, 4]에 +3 // diff = [ 0, 0, 3, 0, 0, -3] diff[2] += 3; diff[5] -= 3; // 구간 [1, 3]에 +2 // diff = [ 0, 2, 3, 0, -2, -3] diff[1] += 2; diff[4] -= 2; // 모든 구간 변화 후 특정 위치의 값 반환 ex. target = 3 // arr[3] = diff[0] + diff[1] + diff[2] + diff[3] = 5 for (int i = 0; i <= 3; i++) { arr[3] += diff[i]; }📊 시간 복잡도
연산 복잡도 구간 갱신 O(1) 전체 복원 O(N) 📚 주요 활용처
- 배열의 특정 구간에 여러 번 값을 더하거나 빼야 할 때
- 업데이트(쓰기)가 많고, 조회는 마지막에 한 번만 필요할 때
3️⃣ 2차원 배열로의 확장
2차원 배열로 누적합과 차이 배열을 확장할 수 있다. 1차원 배열과 같은 원리로, 사각형 범위에 대한 값을 빠르게 얻거나 갱신하고자 할 때 유용하다.
📌 누적합의 2차원 배열 확장
2차원 배열에서 $prefix[j][i]$는 $(0, \ 0)$부터 $(i, \ j)$까지의 사각형 영역의 총합을 의미한다.
$$prefix[j][i] \ = \ matrix[j][i] \ + \ prefix[j \ - \ 1][i] \ + prefix[j][i \ - \ 1] \ - \ prefix[j \ - \ 1][i \ - \ 1]$$
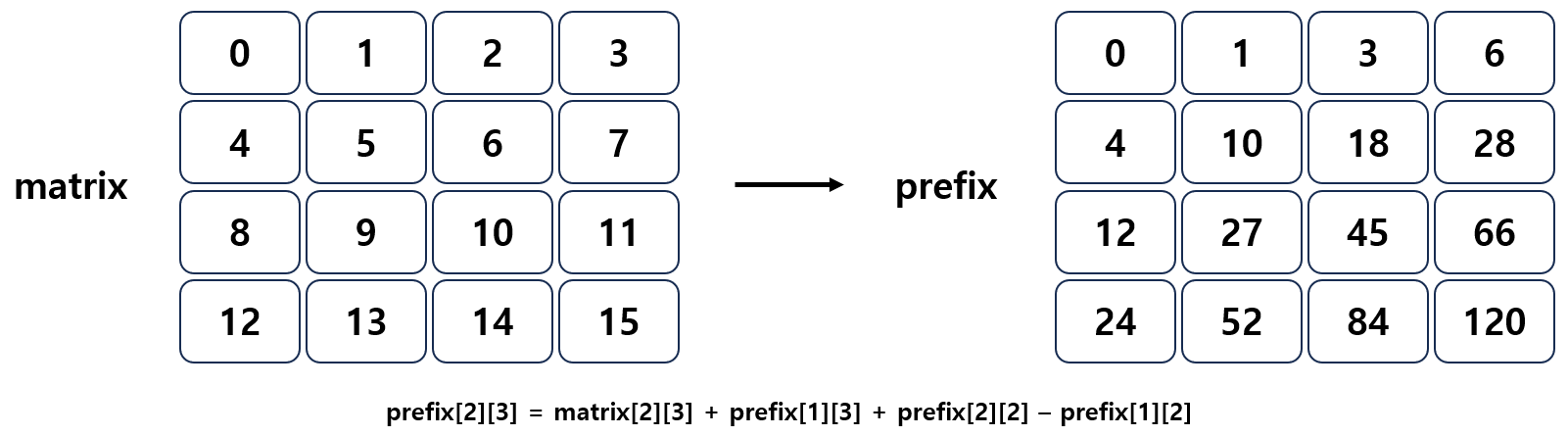
2차원 배열에서의 누적합을 계산한 결과 마찬가지로, 미리 계산한 누적값을 재활용하여 구간 합을 $O(1)$ 시간에 구할 수 있다.
$$sum \ = \ prefix[y2][x2] \ - \ prefix[y1 \ - \ 1][x2] \ - \ prefix[y2][x1 \ - \ 1] \ + \ prefix[y1 \ - \ 1][x1 \ - \ 1]$$
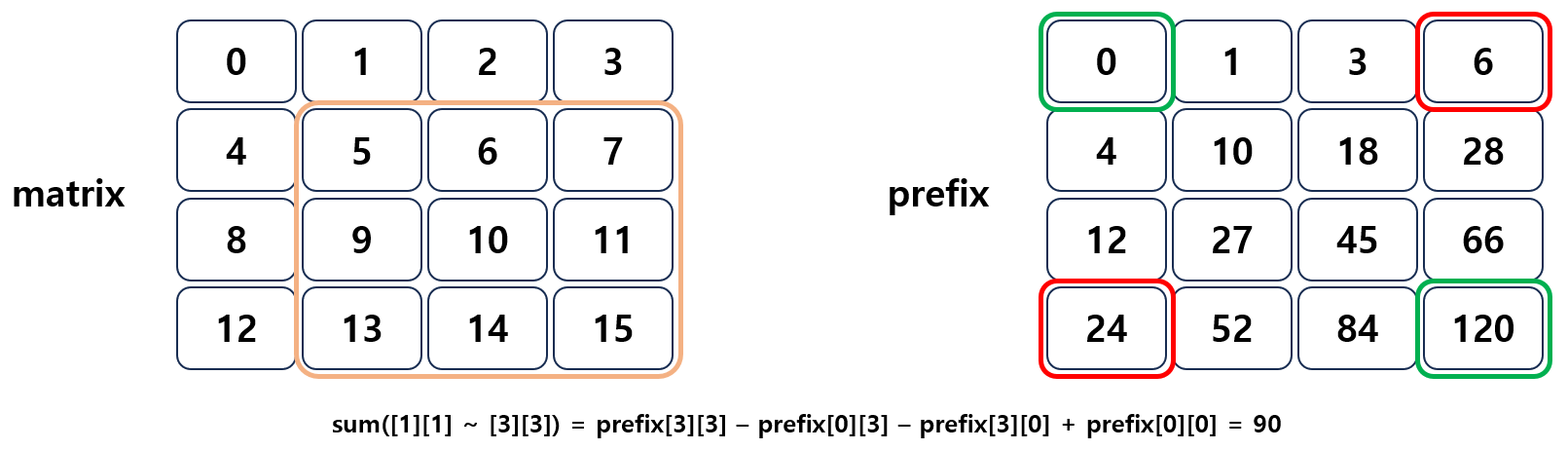
계산한 누적합을 활용하여 구간합을 계산한 결과 🔨 구현 예제
vector<vector<int>> matrix = { { 0, 1, 2, 3 }, { 4, 5, 6, 7 }, { 8, 9, 10, 11 }, { 12, 13, 14, 15 } }; int width = matrix[0].size(); int height = matrix.size(); vector<vector<int>> prefix(height, vector<int>(width, 0)); // 누적합 초기 세팅 prefix[0][0] = matrix[0][0]; for (int y = 0; y < height; y++) { for (int x = 0; x < width; x++) { prefix[y][x] = matrix[y][x]; if (x > 0) prefix[y][x] += prefix[y][x - 1]; if (y > 0) prefix[y][x] += prefix[y - 1][x]; if (x > 0 && y > 0) prefix[y][x] -= prefix[y - 1][x - 1]; } } // 구간 [1, 1]부터 [3, 3]까지의 합 = 5 + 6 + 7 + 9 + 10 + 11 + 13 + 14 + 15 = 90 int sum = prefix[y2][x2]; if (x1 > 0) sum -= prefix[y2][x1 - 1]; if (y1 > 0) sum -= prefix[y1 - 1][x2]; if (x1 > 0 && y1 > 0) sum += prefix[y1 - 1][x1 - 1];📌 차이 배열의 2차원 배열 확장
2차원 배열에서의 $diff[j][i]$는 $(i, \ j)$에서의 변화량을 의미한다.
$$diff[j][i] \ = \ matrix[j][i] \ - \ matrix[j \ - \ 1][i] \ - \ matrix[j][i \ - \ 1] \ + \ matrix[j \ - \ 1][i \ - \ 1]$$
1차원 배열과 마찬가지로 사각형의 각 모서리에만 변화량을 적용하여 구현한다.
$$diff[x1][y1] \ = \ diff[x1][y1] \ + \ k, \ diff[x2 \ + \ 1][y2 \ + \ 1] \ = \ diff[x2 \ + \ 1][y2 \ + \ 1] \ + \ k$$
$$diff[x2 \ + \ 1][y1] \ = \ diff[x2 \ + \ 1][y1] \ - \ k, \ diff[x1][y2 \ + \ 1] \ = \ diff[x1][y2 \ + \ 1] \ - \ k$$
(0, 1)부터 (2, 2) 구간에 +3의 변화량이 주어진 경우 
(0, 0)부터 (1, 2)구간에 -2의 변화량이 주어진 경우 마지막에 변화량의 누적합을 통해 원래 배열을 복원한다.
$$matrix[j][i] \ = \ diff[0][0] \ + \ diff[0][1] \ + \ \cdots \ + \ diff[0][i] \ + \ \cdots \ + \ diff[j][i]$$
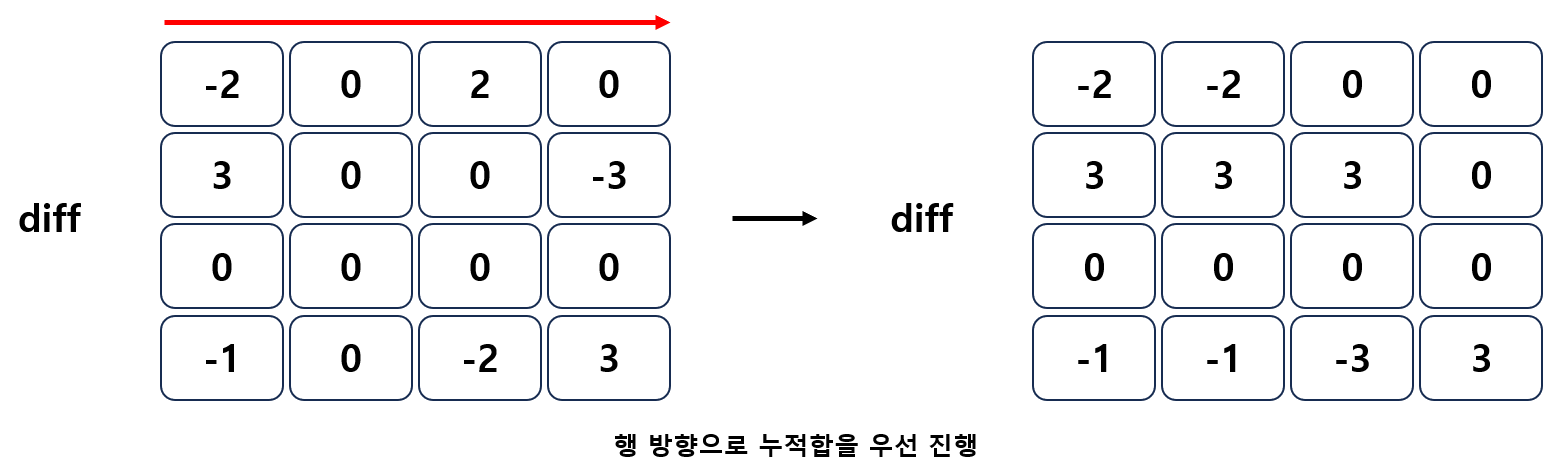
🔨 구현 예제
vector<vector<int>> matrix = { { 0, 0, 0, 0 }, { 0, 0, 0, 0 }, { 0, 0, 0, 0 }, { 0, 0, 0, 0 } }; int width = matrix[0].size(); int height = matrix.size(); vector<vector<int>> diff(height, vector<int>(width, 0); // 구간 [0, 1]부터 [2, 2]에 +3 diff[1][0] += 3; diff[3][3] += 3; diff[3][0] -= 3; diff[1][3] -= 3; // 구간 [0, 0]부터 [1, 2]에 -2 diff[0][0] += -2; diff[3][2] += -2; diff[3][0] -= -2; diff[0][2] -= -2; // 행 방향 누적합 for (int j = 0; j < height; j++) { for (int i = 1; i < width; i++) { diff[j][i] += diff[j][i - 1]; } } // 열 방향 누적합 for (int i = 0; i < width; i++) { for (int j = 1; j < height; j++) { diff[j][i] += diff[j - 1][i]; } }
4️⃣ 추가 사항
❗ 2차원 배열에서 구현 시 주의할 점 - 순서와 안정성
누적합을 계산할 때는 일반적으로 행(가로 방향)을 먼저 누적하고, 그 결과를 기준으로 열(세로 방향)으로 누적한다. 그렇지만, 행과 열의 순서가 바뀌어도 대부분의 경우 결과가 같다.
단, 하나의 전제 조건을 반드시 만족해야 한다. 결합법칙이 성립하는 연산자를 사용하는 경우에만 방향과 상관없이 같은 결과를 출력한다.
또한, 일관성과 디버깅 편의성을 위해 일반적으로 행을 먼저 누적하는 방법이 권장된다.
✅ 누적합과 차이 배열 요약 정리
상황 추천 기법 구간 합을 자주 조회해야 한다. 누적합 (Prefix Sum) 구간에 수를 자주 더하고, 마지막에 한 번만 조회한다. 차이 배열 (Difference Array) 구간 질의가 많은 경우, "빠른 구간 조회"가 필요한 경우 누적합을 사용하고, 구간 갱신이 많은 경우, "빠른 구간 갱신"이 필요한 경우 차이 배열을 사용한다라고 기억하자.
⚡ 누적 연산 구조 - 누적합의 확장
누적합은 덧셈이라는 특정 연산에 대한 누적 처리이다. 덧셈 대신에 다른 결합법칙이 성립하는 연산자를 사용할 수도 있다.
연산자 사용 가능 여부 덧셈 + 예 곱셈 * 예 AND &, OR | , XOR ^ 예 최대 max / 최소 min 예 뺄셈 -, 나눗셈 / 아니오 (결합법칙이 성립하지 않음) 예를 들어, 게임 화면에서 각 픽셀의 빛의 세기를 구간 별로 연산하고 싶을 때, 덧셈 대신 max 연산자를 활용할 수도 있다.