Dynamic Programming

Dynamic Programming of a Recursive Algorithm

• Trade space for speed by storing solutions to sub-problems rather than re-computing them
• Find solutions in a dicionary(table), say soln
• Before any recursive call, search dictionary
• Before returning the solution, store it in the dictionary soln
• Example : fib

fibDPwrap(n)
	Dict soln = create(n);
	return fibDP(soln, n);

fibDP(soln, k)
	int fib, f1, f2;
	if (k < 2) fib = k;
	else
		if (member(soln, k-1) == false) f1 = fibDP(soln, k-1);
		else f1 = retrieve(soln, k-1);
		if (member(soln, k-2) == false) f2 = fibDB(soln, k-2);
		else f2 = retrieve(soln, k-2);
		fib = f1 + f2;
	store(soln, k, fib);
	return fib;

 

Matrix-Chain Multiplication

• Matrix-Chain Multiplication : Given $<A_1, \ A_2, \ \cdots \ , \ A_n>$, Compute $A_1A_2\cdots A_n$
• Matrix $A_i$, has dimension $p_{i - 1} \times p_i$
• Problem : Fully parenthesize the product of matrices minimizing scalar multiplications
• Multiplying two matrices which are $p \times q$ and $q \times r$ -> $p \times r$
  • $pqr$ scalar multiplications
  • $A_1 =30\times 1, \ A_2=1 \times 40, \ A_3=40\times 10, \ A_4=10\times 25$
  • $((A_1A_2)A_3)A_4\ : \ 30\times 1 \times 40 + 30\times 40 \times 10 + 30\times 10\times 25 = 20,700$
  • $A_1(A_2(A_3A_4))\ : \ 40\times 10 \times 25 + 1\times 40 \times 25 + 30\times 1\times 25 = 11,750$
  • $(A_1A_2)(A_3A_4)\ : \ 30\times 1 \times 40 + 40\times 10\times 25+ 30\times 40\times 25 = 41,200$
  • $A_1((A_2A_3)A_4)\ : \ 1\times 40 \times 10+ 1\times 10\times 25+ 30\times 1\times 25 = 1,400$

 

Development

1. Step 1 : The structure of an Optimal Parenthesization

• Split $A_iA_{i+1}\cdots A_j$, into $A_i\cdots A_k$ and $A_{k+1}\cdots A_j$ for some $i \le k \ <j$
• Cost = (Cost of computing $A_i\cdots A_k$) + (Cost of computing $A_{k+1}\cdots A_j$) + (Cost of multiplying them)
• $A_i\cdots A_k$ and $A_{k+1}\cdots A_j$ should be optimal for some $k$

 

2. Step 2 : Recursive solution

• $m[1, \ n]$ : The solution of the problem
• $m[i, \ j]$ : The minimum # of scalar multiplication
• $0$ if $i=j$
• $min\{m[i, \ k] + m[k + 1, \ j] + p_{i-1}p_kp_j\}$ else if $i<j$
• $s[i, \ j]$ : $k$ at which we can split

 

3. Step 3 : Computing the Optimal Costs in a bottom-up (or top-down) fashion

• Input : $p=<p_0, \ p_1, \ \cdots , \ p_n>$
• Auxiliary table $m[1\cdots n, \ 1\cdots n]$ for $m[i, \ j]$ and $s[1\cdots n, \ 1\cdots n]$ for $s[i, \ j]$

printOptimalParens(s,i,j)
	if i = j
		return A[i];
	else if i < j
		printOptimalParens(s, i, s[i,j]);
		printOptimalParens(s, s[i,j] + 1 , j);

 

4. Step 4 : Constructing an Optimal Solution

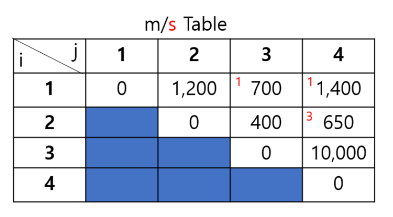
• $A_1 =30\times 1, \ A_2=1 \times 40, \ A_3=40\times 10, \ A_4=10\times 25$
• $A_1((A_2A_3)A_4)\ : \ 1\times 40 \times 10+ 1\times 10\times 25+ 30\times 1\times 25 = 1,400$

1. $m[1, \ 4]$
   • $k = 1 \ : \ m[1, \ 1] + m[2, \ 4] + p_0p_1p_4 = 1,400$
   • $k = 2 \ : \ m[1, \ 2] + m[3, \ 4] + p_0p_2p_4$
   • $k = 3 \ : \ m[1, \ 3] + m[4, \ 4] + p_0p_3p_4$
2. $m[2, \ 4]$
   • $k = 2 \ : \ m[2, \ 2] + m[3, \ 4] + p_1p_2p_4$
   • $k = 3 \ : \ m[2, \ 3] + m[4, \ 4] + p_1p_3p_4=650$
3. $m[3, \ 4]=m[3, \ 3] + m[4, \ 4] + p_2p_3p_4=10,000$
4. $m[2, \ 3]=m[2, \ 2] + m[3, \ 3] + p_1p_2p_3=400$
5. $m[1, \ 2]=m[1, \ 1] + m[2, \ 2] + p_0p_1p_2=1200$
6. $m[1, \ 3]$
   • $k = 1 \ : \ m[1, \ 1] + m[2, \ 3] + p_0p_1p_3=700$
   • $k = 2 \ : \ m[1, \ 2] + m[3, \ 3] + p_0p_2p_3$

Dynamic programming